Simple Linear Regression & Correlation

1. Simple Linear Regression Model

The relationship between study hours (X) and exam grades (Y) is modeled using the simple linear regression equation:

Y = β₀ + β₁X + ε

This model assumes a linear relationship between the predictor variable (study hours) and the response variable (grade), with ε representing random experimental error.

2. Least-Squares Estimation

The regression parameters are estimated using the least-squares method, which minimizes the sum of squared errors (SSE):

SSE = Σ (Yᵢ − Ŷᵢ)²

The slope and intercept estimators are:

β̂₁ = Σ(Xᵢ − X̄)(Yᵢ − Ȳ) / Σ(Xᵢ − X̄)² = 5.0128

β̂₀ = Ȳ − β̂₁X̄ = 39.7469

The fitted regression line is:

Ŷ = 39.7469 + 5.0128X

Interpretation: Each additional hour of study increases the expected exam grade by approximately 5 points.

Grade Predictor

Enter study hours (X) to estimate the expected exam grade using the fitted model: Ŷ = 39.7469 + 5.0128X

Study hours (X)

Predicted grade (Ŷ)

—

3. Inference and Hypothesis Testing

The null hypothesis for the slope is:

H₀: β₁ = 0

The test statistic is:

t = β̂₁ / SE(β̂₁) = 103.72

With 4,998 degrees of freedom, the p-value is far below 0.001, leading to rejection of the null hypothesis. Study hours have a statistically significant effect on exam grades.

95% Confidence Interval for the slope:

(4.918, 5.108)

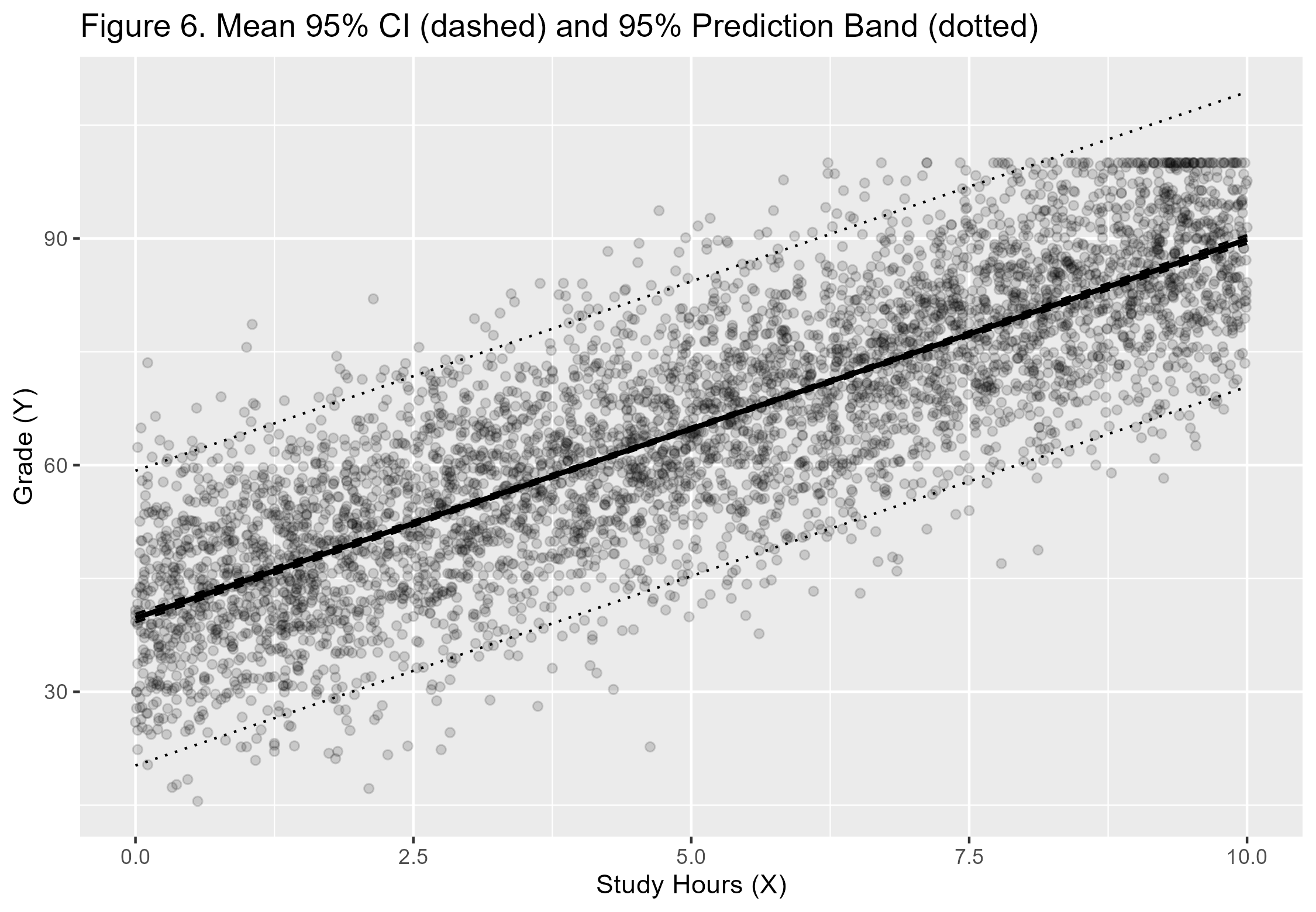
4. Mean Response and Prediction

The estimated mean grade for a fixed study time x₀ is:

Ŷ(x₀) = β̂₀ + β̂₁x₀

Confidence intervals estimate the mean response, while prediction intervals estimate an individual student’s grade.

Prediction intervals are wider because they include individual variability.

5. Correlation Analysis

The Pearson correlation coefficient is:

r = 0.8263

This indicates a strong positive linear association between study hours and exam grades.

The coefficient of determination is:

R² = 0.6828

Approximately 68.3% of the variability in exam grades is explained by study hours.

Figures (Generated in R)

All figures were generated using R and RStudio and correspond directly to the regression diagnostics discussed above.

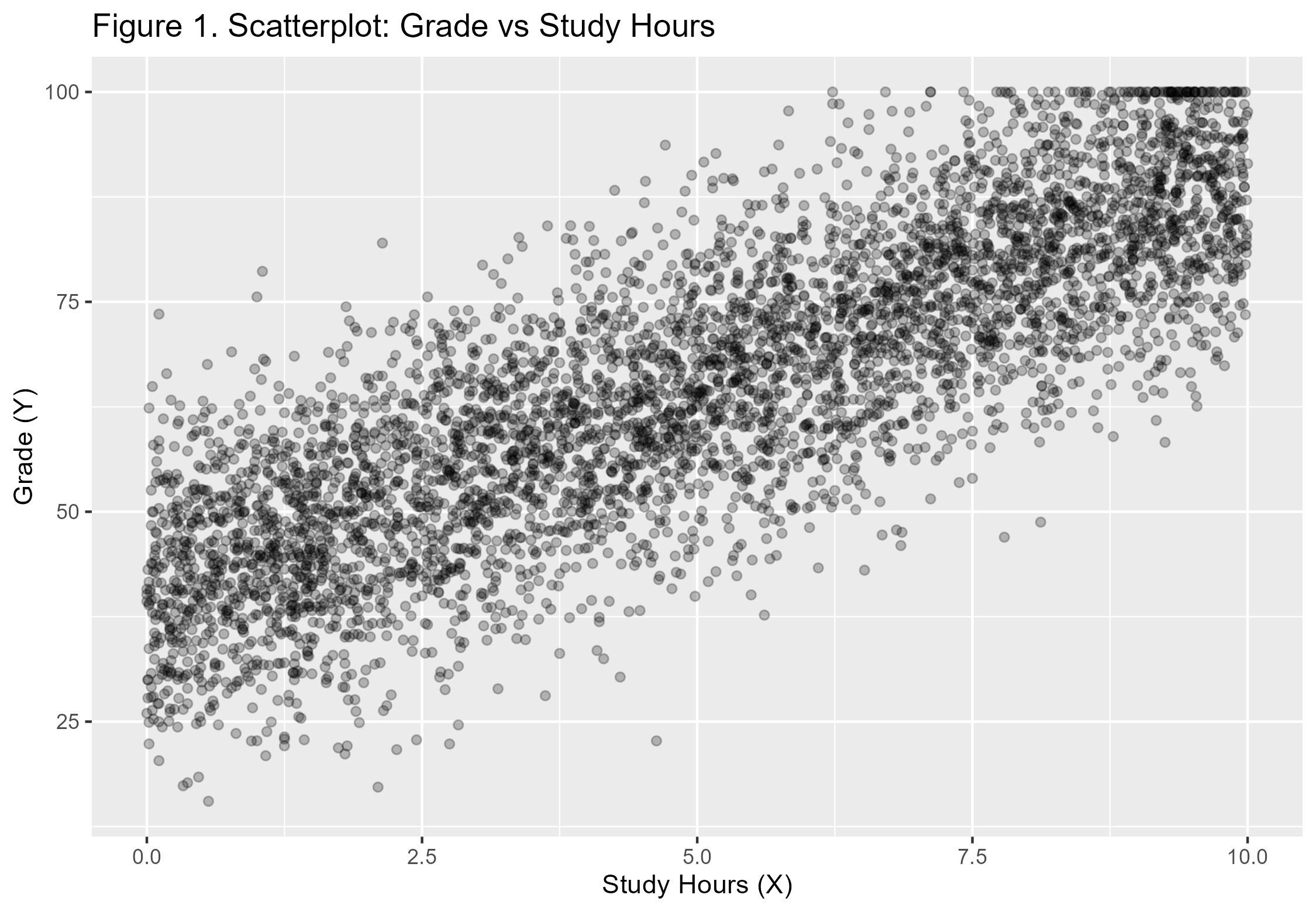
Figure 1 Scatterplot — **Figure 1.** Scatterplot of exam grades versus study hours.

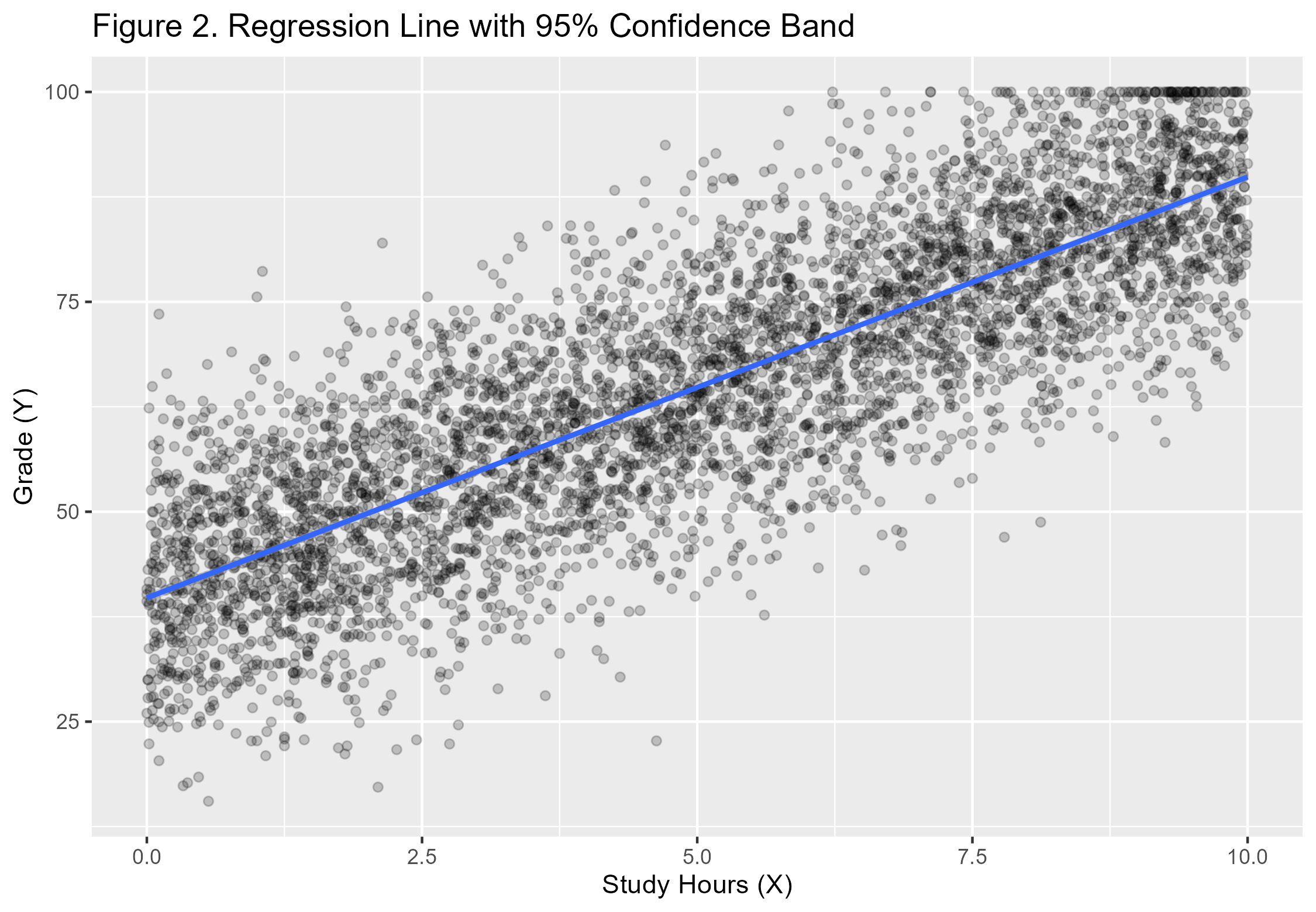
Figure 2 Regression line — **Figure 2.** Fitted simple linear regression line.

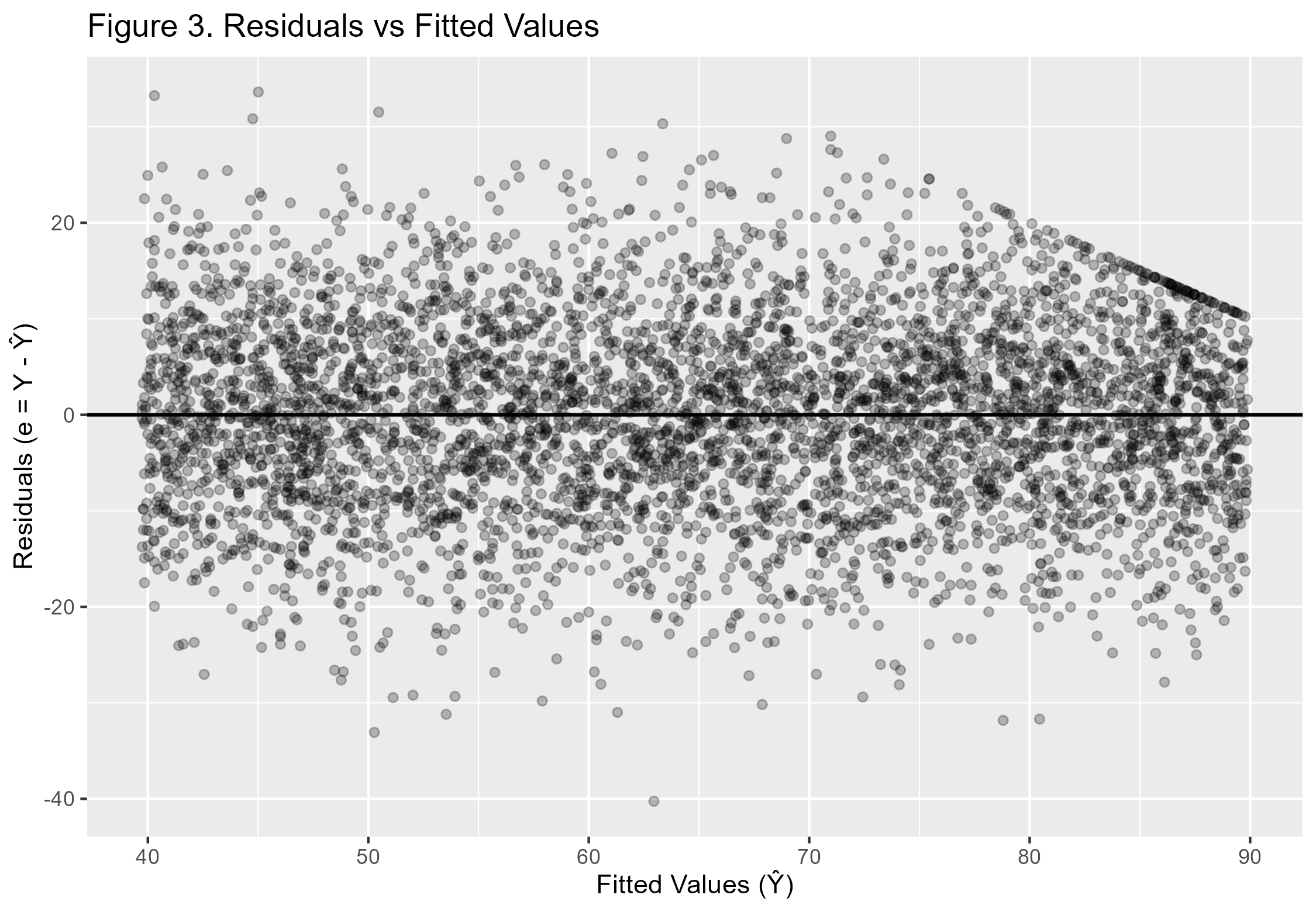
Figure 3 Residuals vs fitted — **Figure 3.** Residuals versus fitted values.

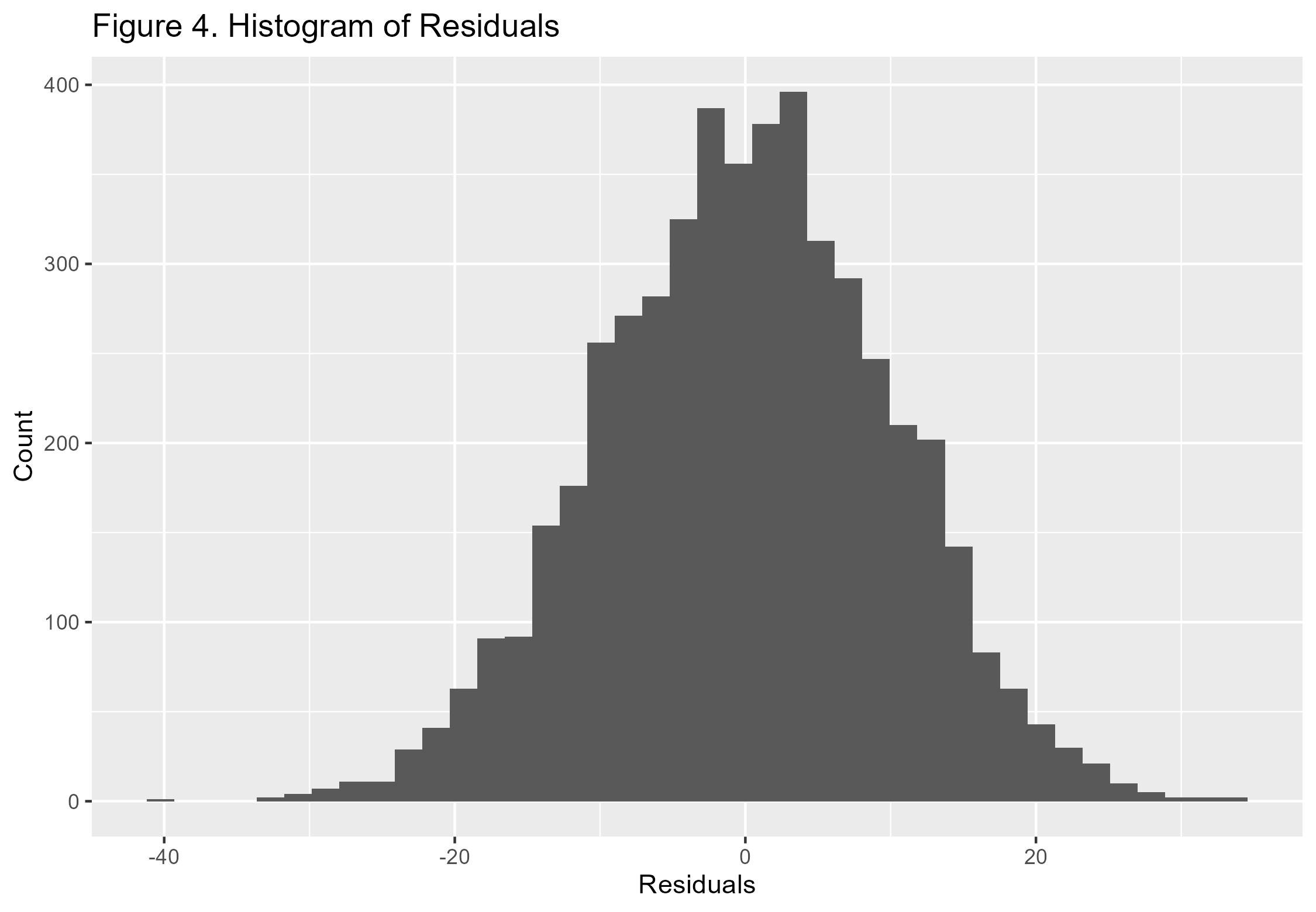
Figure 4 Residual histogram — **Figure 4.** Histogram of residuals.

Figure 5 QQ plot — **Figure 5.** Normal Q–Q plot of residuals.

Figure 6 Bands — **Figure 6.** Mean response CI (dashed) and prediction interval (dotted).

Figure 7 Boxplot — **Figure 7.** Boxplot of exam grades.

6. Conclusion

This project demonstrates how simple linear regression and correlation can be used for modeling, inference, and prediction. The results confirm a strong and statistically significant relationship between study time and academic performance.